When we talk about literacy, we often discuss an initial phase of “learning to read,” which is then followed by a second phase, “reading to learn.” This transition often occurs in grade 3 or 4. To foster literacy acquisition, many states have enacted policies and funded initiatives to ensure that all students are “reading on grade level” by the end of grade 3.

Furthermore, we use the term “emergent readers” when referring to pre-readers. Students are “emergent” until they can decode words with ease. Learning to read English requires students to master a finite set of phonemes (44 in all) and graphemes (around 250). From there, reading—as we well know—shifts to a focus on vocabulary and building knowledge. At this point, we start to refer to students as “readers.”

So, our approach suggests that when students have met the milestone of reading on grade level by the end of grade 3, we feel that they’re on somewhat solid ground. Successfully “learn to read” by the end of grade 3, and then continue to “read to learn” from that point on, and things should turn out fairly well. Reading on grade level by the end of grade 3 is, in other words, the primary benchmark to be met.

This raises some obvious questions. Does mathematics have an equivalent benchmark? When do students transition from being “emergent mathematicians” to being “mathematicians”? Is there some point along the journey where we can begin to feel that students are on a sure footing in math? Several studies have explored this question. Let’s take a look at their findings.

Milestone 1: Mastering elementary math topics

Siegler et al. (2012) explored the relationship between students’ mastery of five major topics in elementary mathematics—addition, subtraction, multiplication, division, and fractions—and their eventual success in high school math courses. Of these five areas, mastery of fractions and of whole-number division were found to be most predictive of eventual high school math success. In fact, knowledge of fractions and whole-number division have a stronger relation to students’ overall math achievement than family income level.

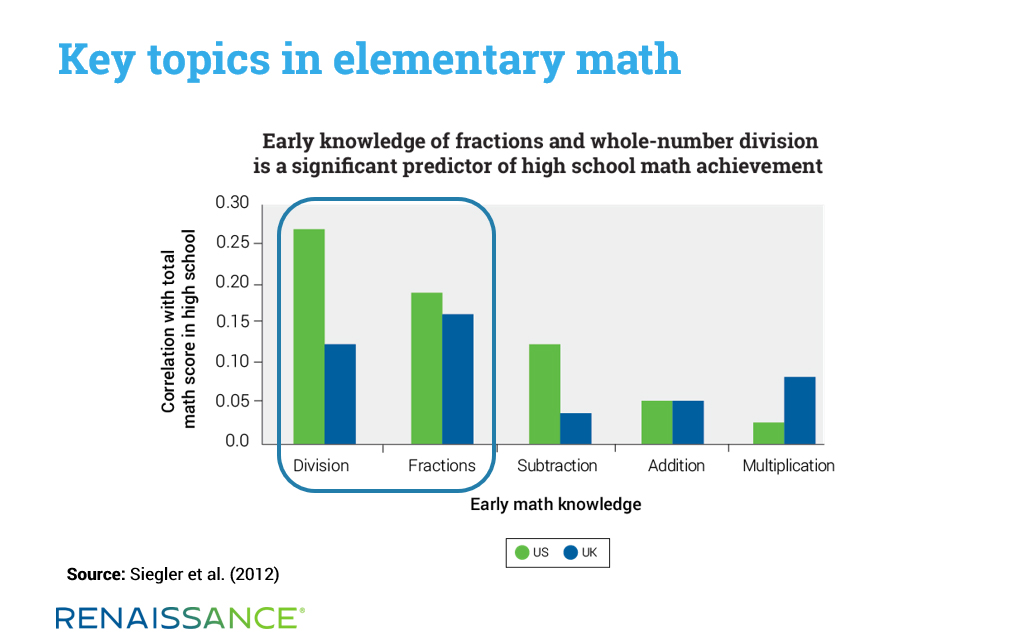
This is not to say that mastery of the other topics—addition, subtraction, and multiplication—is unimportant. In fact, when one considers these topic areas through the lens of learning progressions, it’s apparent that success with division and fractions is dependent on having already mastered addition, subtraction, and multiplication, because these are all prerequisites for division and fractions.

In essence, what Siegler et al. found was that mastering all five topic areas of elementary school mathematics places students in a position where success with high school math courses is far more likely. So, is this the key math milestone? Other studies suggest not.

Milestone 2: Passing grade 6 math

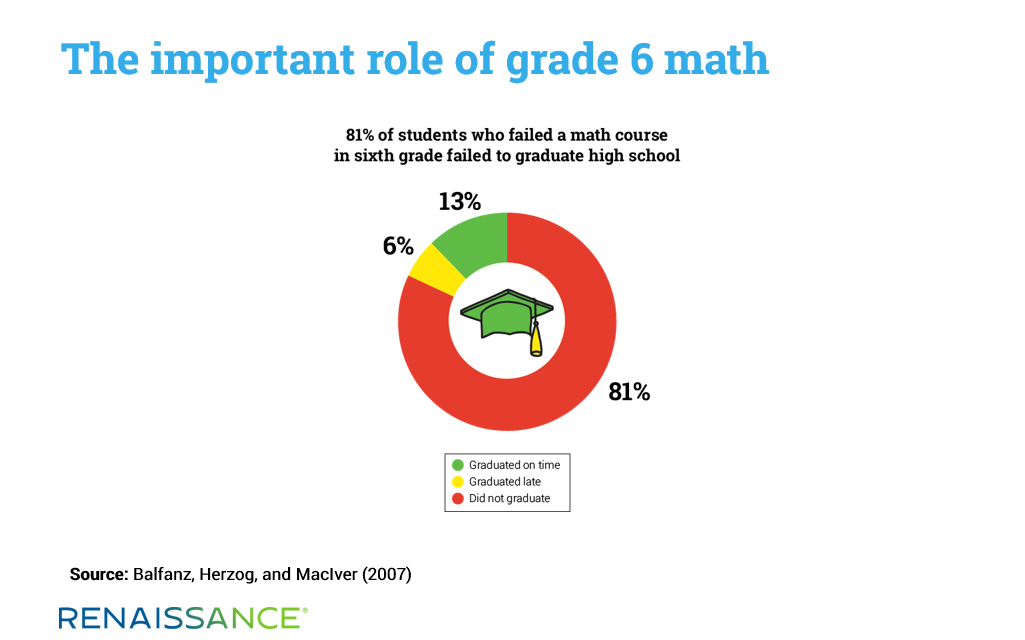
Balfanz, Herzog, and MacIver (2007) conducted a longitudinal study examining the graduation patterns of nearly 13,000 students in an urban district to discover how middle school factors related to high school graduation. They found that a shocking 81 percent of students who failed their grade 6 mathematics course did not graduate from high school. Another 6 percent did graduate, but late. This means that only 13 percent of students who failed their grade 6 math class were able to graduate high school on time—making the passing of grade 6 math extremely predictive of eventual high school graduation. The authors add that “failing a sixth-grade math course was a better predictor of failure to graduate than either a student’s race or status as an English Language Learner.”

Milestone 3: Passing grade 7 math

A study by Finkelstein et al. (2012) further complicates this picture. The authors conducted a longitudinal analysis that tracked more than 24,000 California students from 24 districts from grade 7 through high school graduation. The analysis “looked at the student’s performance in each [math] course, as demonstrated by the grade earned and student proficiency, using as a proxy the student’s score (e.g., Below Basic, Basic, Proficient) on the related California Standards Test for each course.” The authors also explored the results of different “course patterns,” primarily to compare students who took Algebra 1 in grade 8 to students who took Algebra 1 in grade 9.

What did the authors find? “Students who perform well in grade 7 math are likely to take more-advanced courses in high school compared to those who struggle with middle school math.” In fact, of their large sample (N=24,279), “not a single student who earned below a grade of D in seventh-grade math went on to take calculus in high school.”

Does this make grade 7 math the key milestone?

Milestone 4: Passing Algebra 1 on the first attempt

Additional findings by Finkelstein et al. suggest not. They note that while “many students repeat algebra…few repeaters achieve proficiency on their second attempt.” Roughly one-third of the students in their sample were required to repeat their algebra course. Among those who took Algebra 1 in grade 8 and repeated it in grade 9, the eventual proficiency rate on the state test was 21 percent. For those who initially took the course in grade 9 and repeated it in grade 10, the proficiency rate was just 9 percent.

The researchers concluded that “these low proficiency rates illustrate that Algebra 1 repeaters are often unsuccessful at demonstrating content mastery their second time around.” Based on this finding, a reporter highlighting this research began her coverage by stating, “California students who fail algebra and repeat the course are pretty much doomed to fail again” (Tucker 2012).

Are there really any math milestones?

So, where does this leave us? Is there any mathematics equivalent to reading on grade level by the end of grade 3? It appears not. Of the benchmarks outlined above, successfully passing Algebra 1 on the first attempt is probably the first time that we might consider students to be on some degree of solid ground. But Stephen Pinker (1997) said it best when he remarked that “math is ruthlessly cumulative.” And while the importance of mastering prerequisite skills is manifest in all subject areas, no subject area is as “ruthlessly cumulative” as mathematics—as the studies that I’ve described so clearly demonstrate.

What does this mean in terms of instructional practice? It speaks to the need for ongoing formative assessment and progress monitoring—student by student and skill by skill—so that we can ensure the mastery of each and every essential math skill. Otherwise, we risk having this “ruthlessly cumulative” subject area rise up and stifle the progress of the learner.

The power of regular practice—and feedback

Decades ago, when I was a high school student, my teacher for Algebra 1, Algebra 2, and Pre-Calculus would walk up and down the aisle and “spot check” a few key problems from our math homework of the night before. The information she noted in her gradebook was either a check, a check-plus, or a check-minus. This process was time consuming and somewhat flawed, because she was only able to capture limited information on a small portion of the work that we’d done. While our homework had a positive effect on us, with some key changes, it could have been far more effective.

In a classic study, Paschal, Weinstein, and Walberg (1984) conducted a meta-analysis of research on various homework approaches. They found that, overall, homework has a positive effect size of 0.36, but corrected homework has a much larger positive effect size of 0.80. To put this another way: If educators and students aren’t receiving as much information (feedback) as possible from the activities that students undertake, then the impact of those activities is far less than it could be.

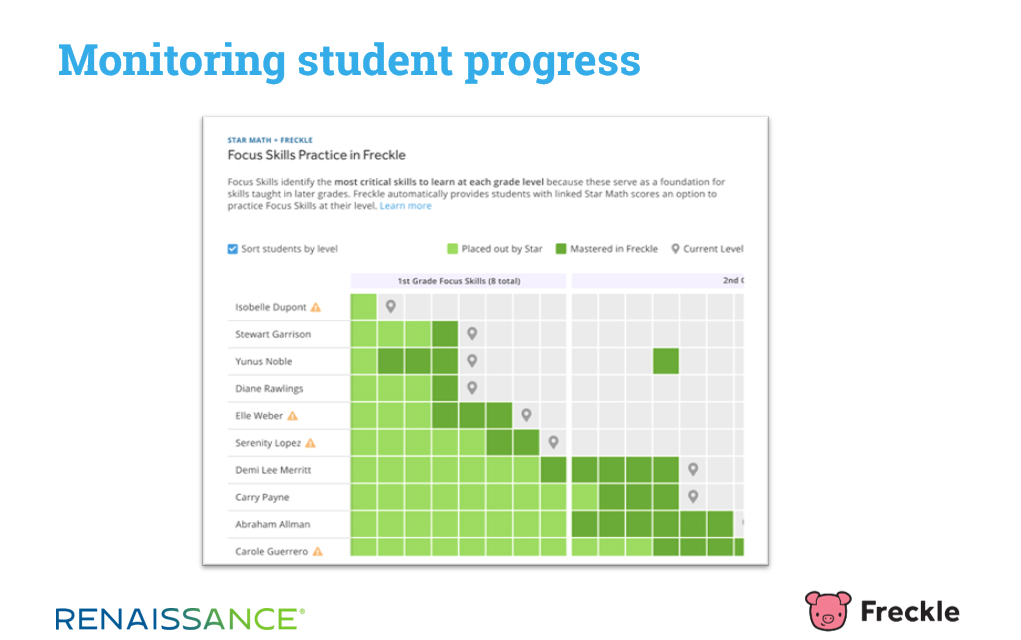
This is where the features of digital math practice programs really shine. With today’s technology, capturing every response from every student to every math problem is easily accomplished. At Renaissance, we offer our Freckle for math program, which provides differentiated practice from kindergarten through Algebra 2. As shown in the screenshot below, teachers using Freckle can easily access a gradebook-like view to see performance student-by-student and skill-by-skill, which is so critical for monitoring students’ progress.

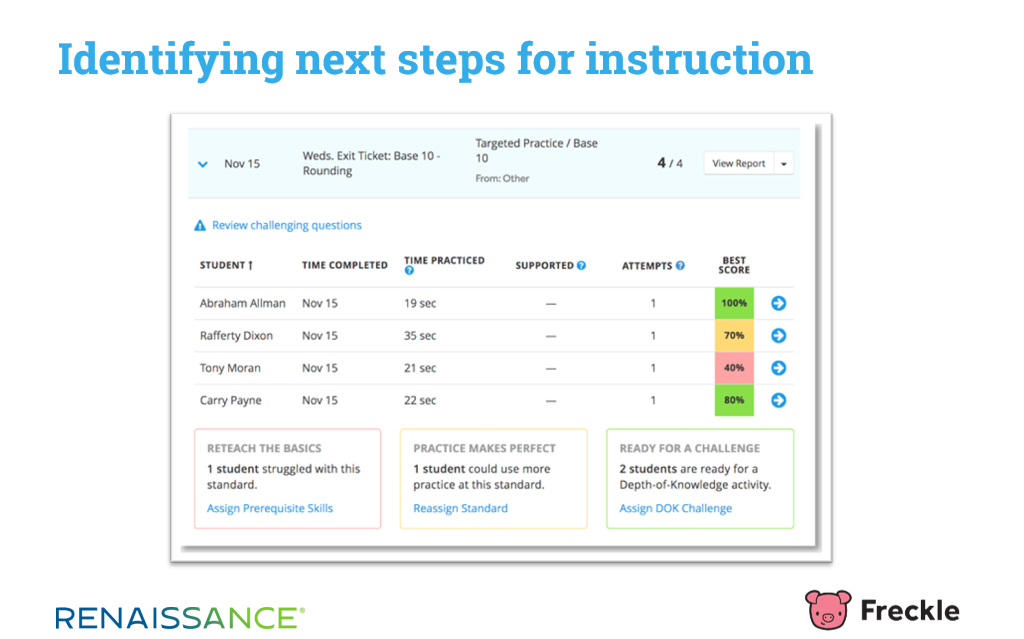
Freckle then makes suggestions for appropriate next steps based on students’ performance. For example, on the screen shown below, teachers can quickly review students’ performance on an “exit ticket” for Base 10—Rounding. Freckle also identifies students who might need some re-teaching of prerequisite skills (in this case, Tony), students who need a bit more practice with the current skills before moving on (Rafferty), and students who are ready for a deeper challenge that probes their Depth of Knowledge (DOK) on the current skill (Abraham and Carry).

Why monitoring progress is key in mathematics

When I was a teacher, I primarily taught one subject area. When I became the Supervisor of Academic Services in my school district, I worked with educators across all content areas—and this is also the case in my role as Chief Academic Officer at Renaissance. Anyone who has made this transition from teaching one subject area to supporting all subject areas knows that you quickly understand how very different the pedagogical concerns and considerations are across areas. What social studies teachers must consider and do is fundamentally different in many ways from what their ELA colleagues or math colleagues or science colleagues must do. Yes, there are common elements of well-crafted instruction, but each content area has its own feel and dynamics.

Given that mathematics is “ruthlessly cumulative”—due to the interdependency of so many discrete skills that must be applied with absolute precision—it simply is a content area in which the close monitoring of student progress, on a detailed level, is paramount. We cannot afford for students to achieve anything less than mastery of essential skills and concepts during the long journey through the various milestones of progress.

Decades ago, my math teachers did what they could to sample and spot-check the work that my classmates and I were doing. But today, a student-by-student and skill-by-skill feed of information can be easily provided by technology, regardless of whether students are practicing math in the school building, at home, or a combination of the two. Our goal should be to ensure that this level of detailed monitoring and feedback is the norm in every math classroom.

References

Balfanz, R., Herzog, L., & MacIver, D. (2007). Preventing student disengagement and keeping students on the graduation path in urban middle-grades schools: Early identification and effective interventions. Educational Psychologist, 42(4), 223–235.
Finkelstein, N., Fong, A., Tiffany-Morales, J., Shields, P., & Huang, M. (2012). College bound in middle school and high school? How math course sequences matter. Sacramento, CA: The Center for the Future of Teaching and Learning at WestEd.
Paschal, R., Weinstein, T., & Walberg, H. (1984). The effects of homework on learning: A quantitative synthesis. The Journal of Educational Research, 78(2), 97–104.
Pinker, S. (1997). How the mind works. New York: Norton.
Siegler, R., Duncan, G., Davis-Kean, P., Duckworth, K., Claessens, A., Engel, M., Susperreguy, M., & Chen, M. (2012). Early predictors of high school mathematics achievement. Psychological Science 23(7), 691–697.
Tucker, J. (2012). Students failing algebra rarely recover. Retrieved from: https://www.sfgate.com/education/article/Students-failing-algebra-rarely-recover-4082741.php