March 22, 2018
Can a student’s math achievement in prekindergarten predict whether they will graduate from college with a bachelor’s degree or higher?
Math is so much more than just numbers and symbols. It’s logic and critical thinking. It’s problem solving. It helps us understand our world in deeper, more meaningful ways. And it may affect how successful we are in that world.
For example, one researcher analyzed the educational outcomes and math scores of several thousand students. After crunching the numbers, he declared that, even without considering any other factors, math achievement alone explained “about a 30% to 60% range of variance in the chance of being on track to college readiness.”1 In his view, math wasn’t the only factor influencing college readiness, but it was one of the more important ones.
This researcher even claimed he could use a student’s math achievement in prekindergarten to determine whether they would stay on track for enrollment at a two-year college, completion of two-year college with an associate’s degree or above, enrollment at a four-year college, or completion of four-year college with a bachelor’s degree or above. As students moved through the grades, he seemed better able to predict how they would track for college outcomes. He concluded that “school math achievement is a good predictor of whether students in P–12 education stay on track toward two-year or four-year college education.”
One researcher has claimed that math achievement is a good predictor of whether a student stays on track for completion of four-year college with a bachelor’s degree or above.
While no other studies have reached the same conclusion—and until much more research is done on the topic, we remain rather doubtful that prekindergarten or even elementary math achievement can accurately predict college graduation—it is clear that there is often a link between math achievement and overall student success.
Considering the critical role math may play in student outcomes, what are the key milestones that students need to stay on track for success?
Elementary math predicts high school achievement
Let’s start at the beginning. Which types of mathematics content knowledge are most essential for elementary-aged children?
The answer is fractions and whole-number division. Mastering these two concepts in elementary school can help students get on the right track for success in high school.
This was the conclusion reached by one study that analyzed the math scores of more than 4,000 children in the United States (ages 10–12) and the United Kingdom (age 10 only) to identify the types of mathematics content knowledge that best predicted students’ long-term learning. In a multiple-regression analysis, fractions and whole-number division were the only two early math concepts that had a significant correlation with students’ overall mathematics achievement in high school in both countries.2
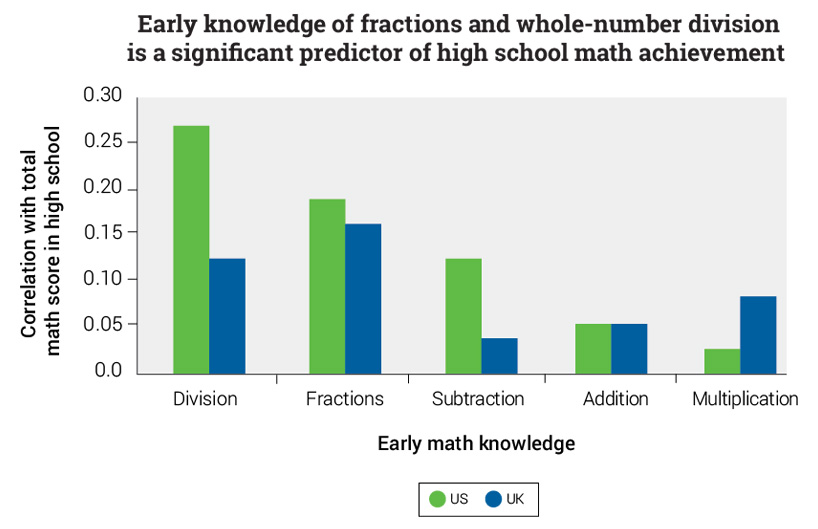
In addition to finding that knowledge of fractions and whole-number division were better predictors of high school math achievement than whole-number addition, subtraction, or multiplication, the study also discovered that knowledge of fraction and whole-number division had a stronger relation to overall math achievement than family income level did.
That’s not to say that educators can skip addition and subtraction and go straight to division and fractions. Addition and subtraction are prerequisites that must be mastered first, before students can advance to more difficult concepts like division and fractions. Instead, these results indicate that students can’t stop at addition and subtraction in elementary; they must strive toward more advanced concepts.
Furthermore, while early knowledge of fractions and division were found to be good predictors of students’ overall mathematics achievement in high school, they were poor predictors of skill in other areas, such as spelling or passage comprehension. The authors also concluded that the “greater predictive power of knowledge of fractions and knowledge of division was not due to their generally predicting intellectual outcomes more accurately.” In other words, measuring these two concepts did not simply identify high-performing students who succeeded in all areas, but predicted math achievement for students of all different ability levels.
Middle school math predicts high school graduation
If elementary school math can predict high school math, what can middle school math predict?
One longitudinal study examined the graduation patterns of nearly 13,000 students in an urban district to discover how middle school factors related to high school graduation. The results showed that only 13% of students who failed a math course in sixth grade graduated on time. An additional 6% graduated one year late. The remaining 81% had not graduated by the time the study ended.3
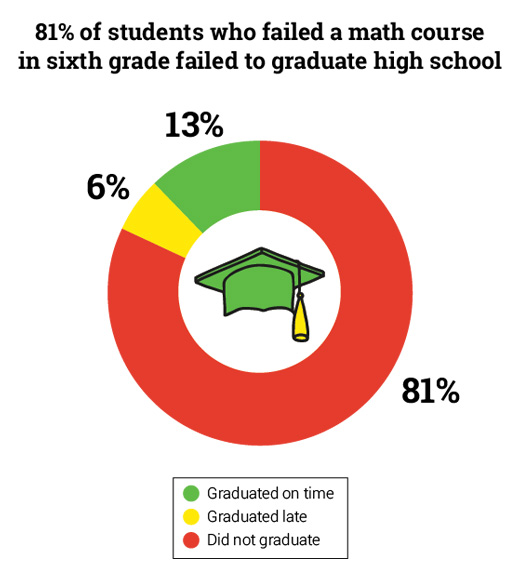
Moreover, failing a sixth-grade math course was a better predictor of failure to graduate than either a student’s race or status as an English Language Learner. In comparison, end-of-sixth-grade test scores were poor predictors of whether a student would drop out.
High school math predicts career goals
When it comes to math achievement, the high school years may be some of the most critical in a student’s academic career. We’re not trying to sound overdramatic, but research indicates a student’s math performance in these grades may affect the rest of their life.
To start with, there appears to be a relationship between high school students’ math achievement and their hopes and dreams for the future. A longitudinal study examined the career aspirations of “high-achieving” ninth graders (who attained 75% or better in their math courses) and “low-achieving” ninth graders (who attained less than 75% in their math courses).
After controlling for students’ perceptions of their own math competence, their overall GPA, and the education levels of their parents, the authors found ninth-grade math achievement had a significant effect on career aspirations—not just in ninth grade but even after high school graduation.4 Math achievement, specifically, seemed to affect career goals above and beyond overall academic achievement.
Low-math-achieving students not only started out with lower occupational aspirations, but also experienced a dramatic decline in their aspirations from mid-high school onward. High-math-achieving students also saw a decline in career aspirations, but started with higher overall aspirations and saw a more gradual decline throughout high school and postsecondary years, ending with career goals notably higher than their low-achieving peers.
Ninth-grade math achievement is a “critical filter” for students’ career goals.
The authors suggested that ninth-grade math achievement is a “critical filter” for students’ career goals and “low math achievement early in high school may steer adolescents away from the advanced math courses required by postsecondary education programs that lead to many higher-prestige career paths, not only in the physical science and technology fields, but also in health, commerce, and many social sciences.”
As we’re about to see, those advanced math courses in high school are particularly important when it comes to college and career outcomes.
High school math predicts college graduation, postsecondary degrees, and career earnings
A report that examined the long-term outcomes of thousands of students across the United States found clear connections between the highest level of math completed by the end of high school and the highest degree of education attained 10 years later.5 Only 3% of students who had completed vocational math but no higher-level math courses had earned a bachelor’s degree or higher, whereas 73% of students who had completed at least one calculus course held a bachelor’s degree or higher.
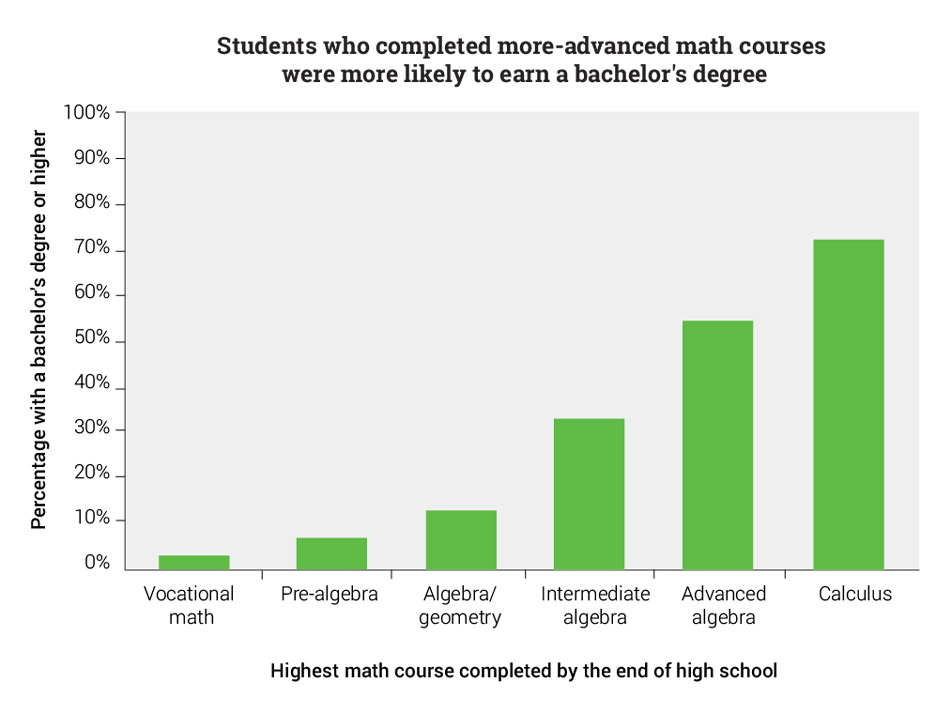
Furthermore, students who did not complete more-advanced math courses such as algebra or calculus were much more likely to drop out of high school or fail to earn a high school diploma.
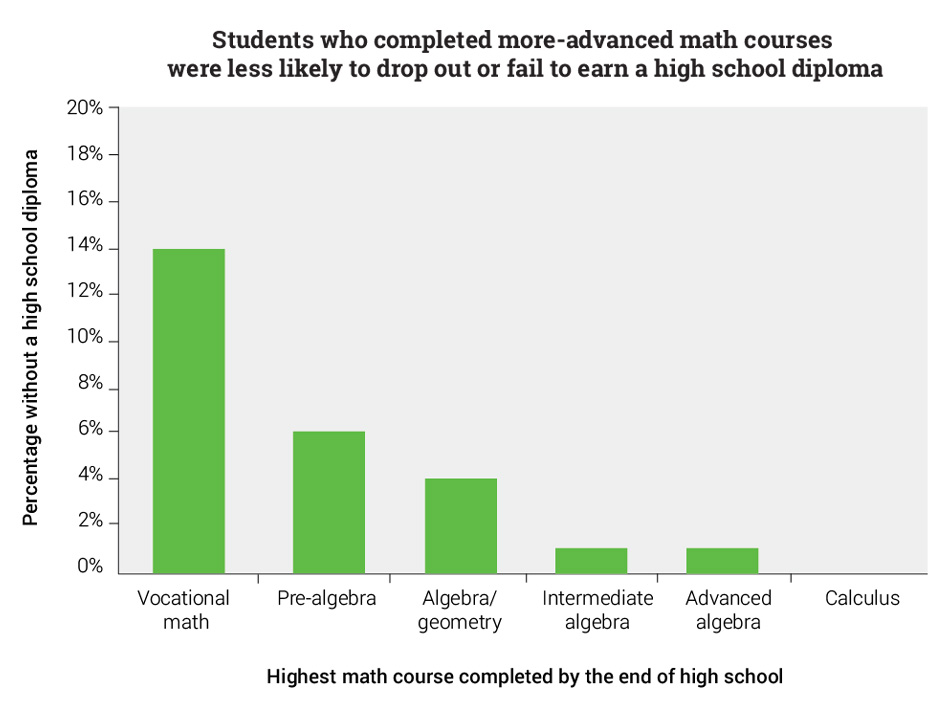
For all ethnicities and all income levels, the higher the level of math courses a student completed, the more likely they were to graduate college with a bachelor’s degree. Completion of more-advanced math courses increased the predicted probability of college graduation even when the authors controlled for demographic traits, socioeconomic status, family and school characteristics, and overall measures of math ability (i.e., math GPA and grade 10 math test score).
Even 10 years after high school, math curriculum had an effect on annual earnings. Students who had completed a calculus course earned 65% more than students whose math education did not progress past a vocational math course. After accounting for ethnicity, gender, and other demographic traits; parental education and income; and high school characteristics, more-advanced mathematics courses still had an effect on annual earnings.
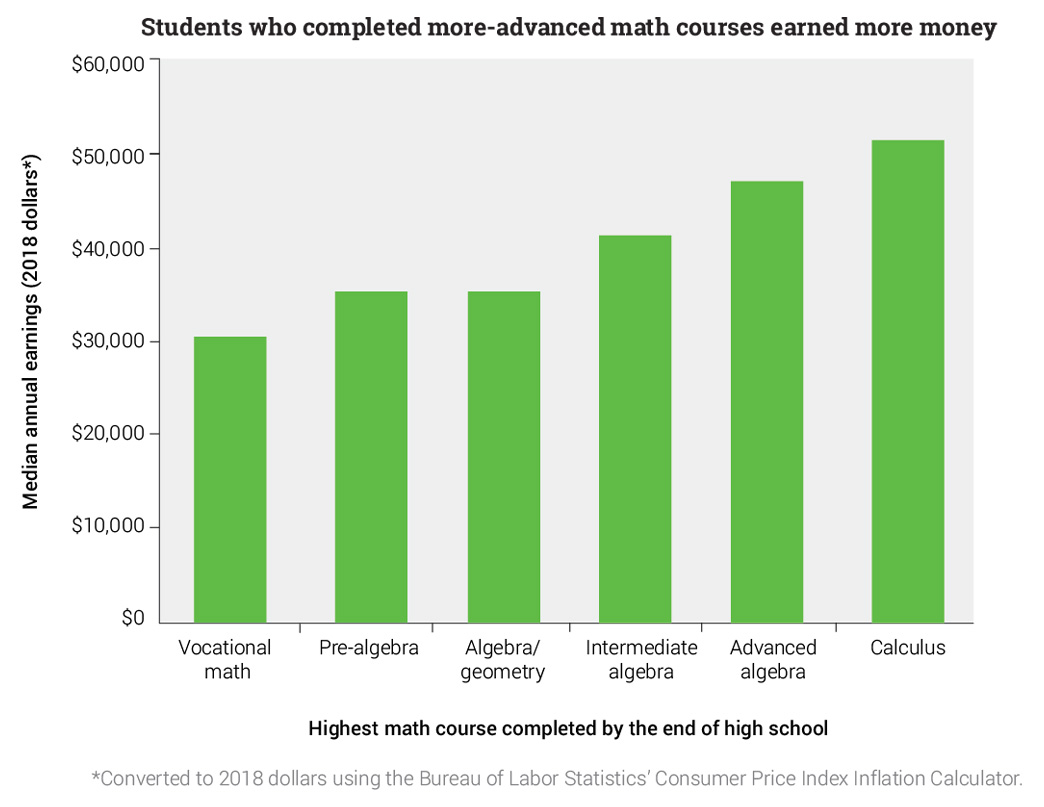
Moreover, math curriculum continued to have “striking” effects on earnings even after controlling for highest degree earned and college major as well as demographics, family, and school, suggesting that “there is a direct effect of math curriculum on labor market productivity, which works independently of the final degree attained.” Following this logic, if there were two individuals of the same ethnicity and gender, who come from similar families and attended the same high school, who both have the same degree in the same field (say a bachelor’s degree in biology), the one who completed a calculus course by the end of high school would likely earn more money than the one who did not!
On top of that, math courses still seemed to have an effect on earnings when courses taken in other subjects were considered. Advanced-level English courses increased earnings, but not as much as advanced algebra or calculus did. In addition, algebra/geometry, intermediate algebra, advanced algebra, and calculus all appeared to increase earnings more than average-level English courses did.
Note that for all these analyses, the total number of math courses completed wasn’t the key factor—it was the level of those courses. As the authors put it, “it is not simply the number of math courses that matters; what matters more is the extent to which students take the more demanding courses, such as algebra/geometry.”
Math’s path to college and career readiness
We’ve seen how math milestones can help students get on the path to college and career success. From mastering fractions and whole-number division by the end of elementary school to completing more-advanced math courses by the end of high school, each milestone a student achieves is one step closer to success in school and in life.
What does the overall path look like for students? Returning to the first study examined in this post, that author concluded that state standards (as they existed in 2007) were a good starting point.1 When he looked at the math achievement trajectories that led to completion of college, he found that attaining the typical state standard of math proficiency would put students on track for earning an associate’s degree or above from a two-year college. Students who met or exceeded National Assessment of Educational Progress (NAEP) proficient level for math or Trends in International Mathematics and Science Study (TIMSS) high benchmark for math were likely to earn a bachelor’s degree or above from a four-year college.
Considering that only 40% of fourth-grade students, 33% of eighth-grade students, and 25% of twelfth-grade students scored proficient or above on the 2015 NAEP math assessment,6 this may seem like a high bar to reach—but it’s not impossible.
Students can move toward college and career readiness incrementally, one math concept at a time. An analysis of students in grades 3–8 using a research-based math practice program found that 42% of the students who mastered an average of one to three subskills weekly reached college- and career-readiness benchmarks. In comparison, only 33% of the typical students—who did not use the program—were college and career ready. The highest level of college and career readiness was seen among students using the program who averaged mastery of four or more subskills per week; 58% of these students met proficiency benchmarks—almost double the rate of the typical students.
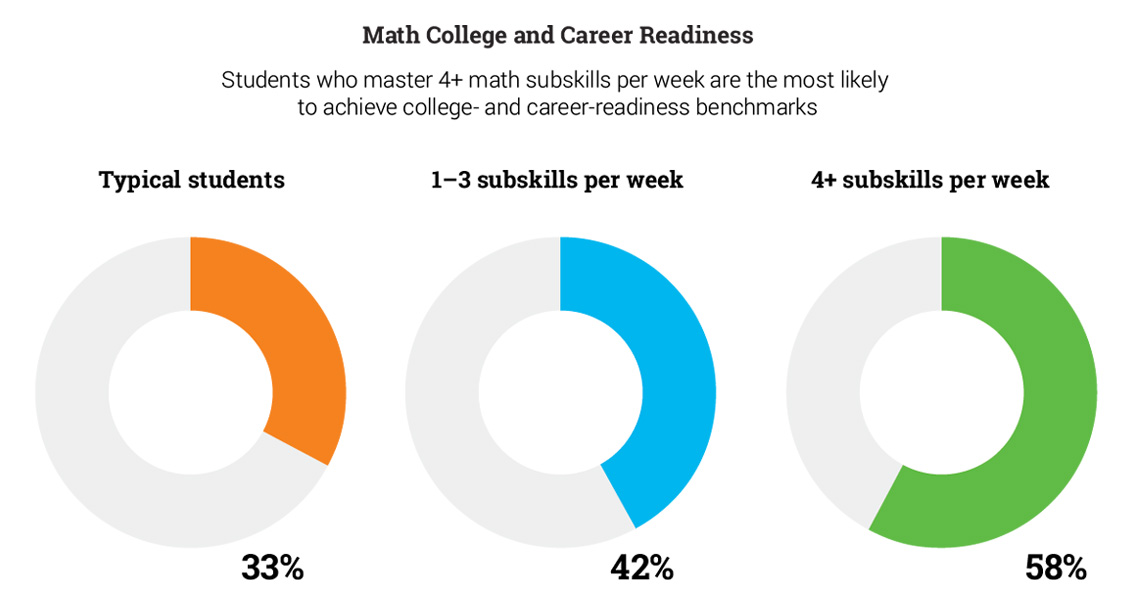
References
1Lee, J. (2012). College for all: Gaps between desirable and actual P–12 math achievement trajectories for college readiness. Educational Researcher, 41(2), 43-55.
2Siegler, R. S., Duncan, G. J., Davis-Kean, P. E., Duckworth, K., Claessens, A., Engel, M., Susperreguy, M. I., & Chen, M. (2012). Early predictors of high school mathematics achievement. Psychological Science 23(7), 691-697.
3Balfanz, R., Herzog, L., & Mac Iver, D. (2007). Preventing student disengagement and keeping students on the graduation path in urban middle-grades schools: Early identification and effective interventions. Educational Psychologist, 42(4), 223–235.
4Shapka, J. D., Domene, J. F., & Keating, D. P. (2006). Trajectories of career aspirations through adolescence and young adulthood: Early math achievement as a critical filter. Educational Research and Evaluation, 12(4), 347-358.
5Rose, H., & Betts, J. R. (2001). Math matters: The links between high school curriculum, college graduation, and earnings. San Francisco, CA: Public Policy Institute of California.
6National Center for Education Statistics. (2015). National Assessment of Educational Progress (NAEP) 2015 mathematics assessments. Digest of Education Statistics. Washington, DC: U.S. Department of Education Institute of Education Sciences. Retrieved from: https://www.nationsreportcard.gov/
7Renaissance. (2017). Trends in student outcome measures: The role of individualized math practice. Wisconsin Rapids, WI: Author.

